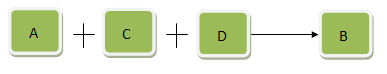# 数学 (必修) 第一册 A 版 (2021)

第 1 章集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
  - 阅读与思考: 集合中元素的个数
- 1.4 充分条件与必要条件
  - 阅读与思考几何命题与充分条件、必要条件
- 1.5 全称量词与存在量词
- 小结
- 复习参考题 1
第 2 章二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 小结
- 复习参考题 2
第 3 章函数的概念与性质
- 3.1 函数的概念及其表示
  - 阅读与思考: 函数概念的发展历程
- 3.2 函数的基本性质
  - 信息技术应用: 用计算机绘制函数图象
- 3.3 幂函数
  - 探究与发现: 探究函数的图象与性质
- 3.4 函数的应用（一
- 文献阅读与数学写作: 函数的形成与发展
- 小结
- 复习参考题

# 生词

intersection /ˌɪntə'sekʃn/ --n.交集；十字路口；交叉点
- intersection set. 交集
- You are gonna make a right at the intersection. 十字路口往右转。
- Turn right at the next intersection. 在下个十字路口右转。
complementary /kɒmplɪ'ment(ə)rɪ/ --adj.补充的，互补的
- complementary set 补集
- complementary angles 余角，互余角
- complementary function 余函数
radical /'rædɪk(ə)l/ --n.根号,根式。 --adj.根本的,基本的
radicand /'rædɪkænd/ n.被开方数。
exponential /ˌekspə'nenʃ(ə)l/ --n.指数. --adj.指数的
- Exponential growth. 指数生长
- exponential function 指数函数
logarithmic /ˌlɔɡə'riðmik/ --adj.对数的
- Logarithmic functions 对数函数

# ▲ 第 1 章集合与常用逻辑用语

汉语词典 解释如下：

# 集合[ jí hé ]

(1) 分散的人或事物聚集到一起；使聚集。

例：紧急集合。

英：assemble; collect; congrate; converge; muster; rally; gether; call together;

(2) 一组具有某种共同性质的数学元素。

例: 有理数的集合。

英: aggregate /ˈæɡrɪɡət/ --n.总数，合计。--adj.总计的，合计的。--v.总计，合计。

标题：集合链接：https://cidian.qianp.com/ci/%E9%9B%86%E5%90%88

# 1.1 集合的概念

一般地，我们把研究对象统称为元素 (element), 把一些元素组成的总体叫做集合 (set)，简称为(集)

只要构成两个集合的元素是一样的，我们就称这 2 个集合是相等的。

我们们通常用大写拉丁字母 ... 表示集合；用小写拉丁字母 ... 表示集合中的元素。

如果是集合中的元素，就说属于(belong to) 集合 , 记作。

如果不是集合中的元素，就说不属于(not belong to) 集合 , 记作。

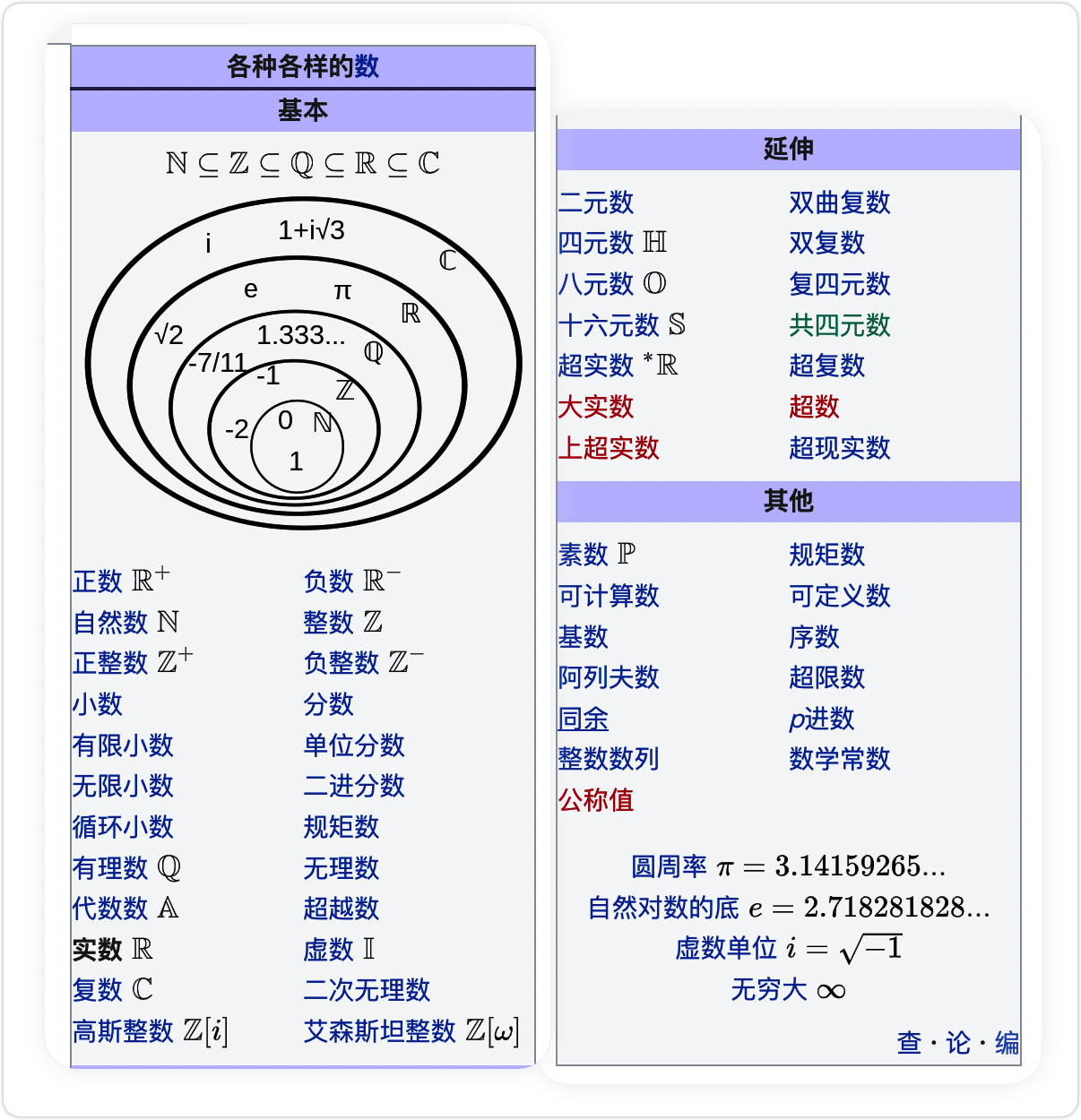
数学的数	概念	符号	示例
自然数	全体非负整数组成的集合称为非负整数集 (或自然数集)
正整数	所有正整数组成的集合称为正整数集	或
整数	全体整数组成的集合称为整数集
有理数	全体有理数组成的集合称为有理数集
	人们将所有能表示成 ( 是整数互质)的数称之为有理数。 - 任何带有 "有限小数部分" 或 "无限循环小数部分" 的数都可以写成的形式，因而都是有理数;		(/)
无理数	人们将不是有理数的数称为无理数。 - 带有无限不循环小数部分的数不能写成的形式，因而是无理数。		wiki-无理数 (opens new window)
实数	（将有理数和无理数统称为实数。）全体实数组成的集合称为实数集。

TIP

Add Information:

下图来源 Wiki: https://zh.wikipedia.org/wiki/%E5%AE%9E%E6%95%B0

TIP

集合的读法:

例如:

读作: 集合 = 集合属于且（不确定对不对,因为没找到范例）

# 添加信息 (Add Information)

名词	符号	解释
质数(又称素数)		质数是大于 1 的自然数中，除了 1 和它本身外，不能被其他自然数 (0 除外) 整数的数。
互质 (co-prime)		又称互素、在数论中，如果 2 个或 2 个以上的整数的最大公因数是 1，则称它们为互质。 (1) 如果数域是正整数(), 那么 1 与所有正整数互质。 (2) 如果数域是整数(), 那么 1 和 -1 与所有整数互质, 而且他们是唯一与 0 互质的整数。兩個整数 a 与 b 互质，记为 a ⊥ b。互质的例子: 例如 8 与 10 的最大公因数是 2，不是 1，因此他们并不互质。又例如 7, 10, 13 的最大公因数是 1，因此他们互质。
有理数		-
无理数
实数(R)
实数系		全体实数组成的数集称为实数系，也称为 "实数集"。
实数的连续性		实数这种能与数轴上的点一一对应的特点称为实数的连续性。

# 1.2 集合间的基本关系

子集 (subset)：或

文氏图 (Venn 图)：在数学中，我们经常用平面上封闭曲线的内部代表集合，这种图称为 Venn 图。

相等：集合与集合中的元素是一样的，说集合和集合相等，记作:

真子集（proper subset）:

: 读作集合真包含于集合，即集合是集合的真子集（注：有的书上符号是在包含于符号下方加不等号）。

真包含的意思是：集合中的元素全部在集合中，而集合中除了与中相同的元素以外，还有其他元素。换言之，集合比集合小（注：此句不是严谨表述，注意取舍）。

空集 (empty set)：把不包含任何元素的集合叫做空集。

# 1.3 集合的基本运算

并集 (union set):

一般地，由所有属于集合或属于集合的元素组成的集合，称为集合与集合的并集 (union set), 记作 (读作: A 并 B), 即:

或

交集 (intersection set):

一般地，由属于集合且属于集合的所有元素组成的集合，称为与的交集 (intersection set), 记作 (读作: A 交 B), 即:

且

全集 (universe set):

一般地，如果一个集合含有我们所研究问题中涉及的所有元素，那么就称这个集合为全集 (universe set), 通常记作

补集 (complementary set):

对于一个集合 , 在全集中不属于集合的所有元素组成的集合称为集合相对于全集的补集 (complementary set)，简称为集合的补集，记作 = $且$

阅读与思考

#### 阅读与思考: 集合中元素的个数

# 1.4 充分条件与必要条件

Added Notes:

我们先来看看 汉语词典 对充分和必要的解释：

(1) 充分：（形容词）充足；多（多用于抽象事物）。例如：有充分的根据。

(2) 必要：（形容词）不可缺少；非这样不可。例：采取一切必要的步骤。/ 研究补助金是必要的。

补充讲解：https://www.zhihu.com/question/30469121

充分条件：

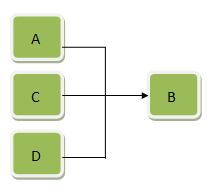
如果条件A是结论B的充分条件：A与其他条件是并连关系，即A、C、D….中任意一个存在都可以使得B成立（就像是个人英雄主义），如下图：

用法：

1．如果条件A存在，B肯定成立，即A→B（箭头表示能够推导出）

2．如果B不成立，则说明所有可能的条件都不存在，因此A肯定也不存在，即非B→非A

3．如果条件A不存在，而条件C、D可能存在，也可以使得B成立，即不能导出非A→非B

必要条件：

条件A是结论B的必要条件：A与其他条件是串联关系，即条件A必须存在，且条件C、D….也全部存在才可能导致B结论。（团结的力量）如下图：

用法：

我简单表示为A+…→B(中间的点表示还有其他条件)

1．如果B成立了，说明所有条件都存在，肯定存在条件A。即B→A。

2．如果条件A不存在，串联少了一个条件，B也肯定不能成立，即 非A→非B。

3．如果B不成立，可能是C，D不存在但A存在，只是C、D掉链子了，即不能导出非B→非A。

# (1) 充分条件与必要条件

# (2) 充要条件

# 阅读与思考几何命题与充分条件、必要条件

# 1.5 全称量词与存在量词

# Add Information:

# 全称量词 / 全称量化

来源: https://zh.wikipedia.org/zh-cn/%E5%85%A8%E7%A7%B0%E9%87%8F%E5%8C%96

全称量词 : 就是 A(ll) 的反写,读作 for all. 表示任意的,所有的.

在谓语逻辑中, 全称量化是尝试形式化某个事物 (逻辑谓词) 对于所有事物或所有有关的事物都为真的概念. 结果的陈述是全称量化后的陈述,我们在谓词上有了全称量化. 在符号逻辑中,全称量化 () 是用来指示全称量化的符号.

# 基础

假设你要说的是: $以及以及$ 等等. 由于 "以及" 一词的重复使用,这似乎是一个 逻辑合取. 然而 形式逻辑 中的合取概念却不能表达出 "等等" 一词的含义. 因此该命题改述为: + 对任意自然数 n, 都存在 .
这便是一个使用全称量化的单一命题.

# 存在量词 ()

存在量词 : 读作 there exists, 就是 E(xistence) 的反写. 表示存在一个, 至少一个.

# 1.5.1 全称量词和存在量词

# 1.5.2 全称量词命题和存在量词命题的否定

# 小结

# 复习参考题 1

# ▲ 第 2 章二次函数、方程和不等式

# 2.1 等式性质与不等式性质

# 2.2 基本不等式

# 2.3 二次函数与一元二次方程、不等式

# 小结

# 复习参考题 2

# ▲ 第 3 章函数的概念与性质

# 3.1 函数的概念及其表示

(一般地，) 设 , 是非空的数集，如果按照某种确定的对应关系 , 使对于集合中任何一个数 , 在集合中都有唯一确定的数 (或说）和它对应，那么就称 : 为从集合到的一个 函数 (function), 记作:

其中叫做自变量，的取值范围叫做函数的 定义域 (domain),

与的值相对应的值叫做函数值, 函数值的集合 { } 叫做函数的**值域 (range)**.

显然，值域是集合的子集。

: 读作: 集合 $且$ 属于 A

我们所熟悉的一次函数的定义域是，值域也是，对于中的任意一个数 , 在中都有唯一的数和它对应。

二次函数的定义域是 , 值域是 .

当时，
- 读作：集合 = 集合且
当时，

对于中的任意一个数 , 在中都有唯一的数和它对应。

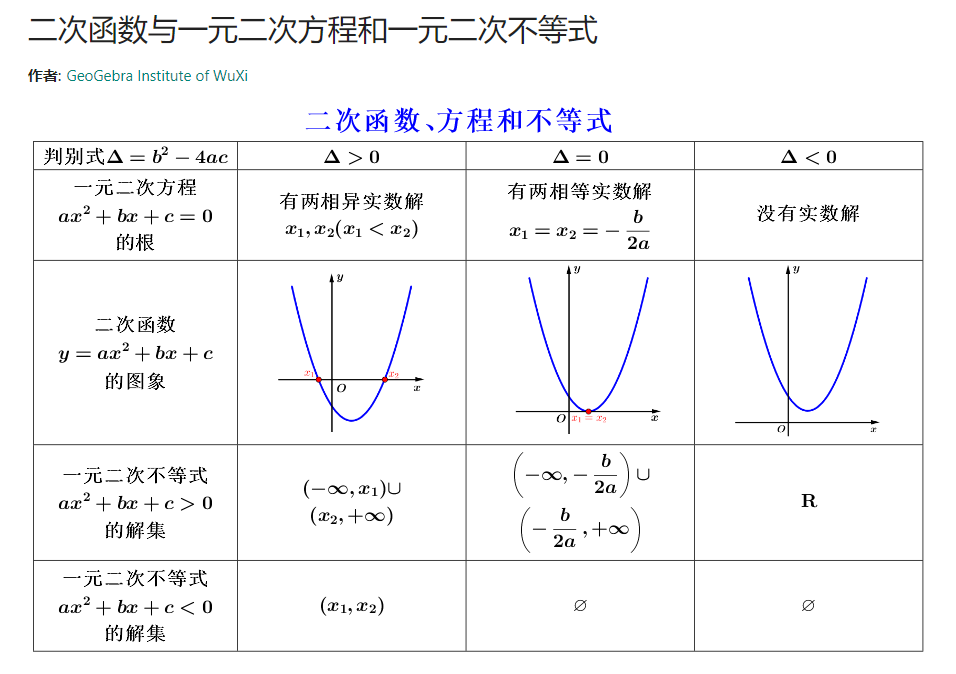
一元二次方程 —— (根的) 判别式:

根的判别式是判断方程实根个数的公式，在解题时应用十分广泛，涉及到解系数的取值范围、判断方程根的个数及分布情况等。一元二次方程的根的判别式是，(用 "" 表示，读作 "delta")。

判别式定义: 判别式即判定"方程实根"个数及分布情况的公式。

一元二次方程，根的判别式的推导过程: (20200202 Added: 来自九年级上册课本 P28)

解: 因为一元二次方程的 , 所以两边同除以

移 项 得 配 方 一 次 项 系 数 一 半 的 平 方 得 即 因 为 所 以 当 时 直 接 开 平 方 得 当 时 当 时

这里的叫做一元二次方程**根的判别式**, 通常用符号来表示, 用它可以直接判断一元二次方程的实根的情况:

当时, 方程有 2 个不相等的实数根;
当时, 方程有 2 个相等的实数根;
当时, 方程没有实数根.

区间:

闭区间:
开区间:
半开半闭区间: [a, b), (a, b]
端点: 用实心点表示包括在区间内的端点，用空心点表示不包括在区间内的端点。

分段函数

映射 (mapping): 设 , 是非空的集合，如果按某一个确定的对应关系，使对于集合中的任意一个元素，在集合中都有唯一确定的元素与之对应，那么就称对应为从集合到集合的一个映射 (mapping).

# 阅读与思考: 函数概念的发展历程

# 3.2 函数的基本性质

# 1.3.1 函数的基本性

增函数 (increasing function)
减函数 (decreasing function)
最大值 (maximum value)
最小值 (minimum value)
奇函数 (odd function)
偶函数 (even function)

# 信息技术应用: 用计算机绘制函数图象

# 3.3 幂函数

详细见: <托马斯微积分> 1.1.6 幂函数

# 探究与发现: 探究函数的图象与性质

# 3.4 函数的应用（一）

# 3.1 函数与方程

# 3.1.1 方程的根与函数的零点

二次函数的定义域是 , 值域是 .

当时，
当时，
对于中的任意一个数 , 在中都有唯一的数和它对应。

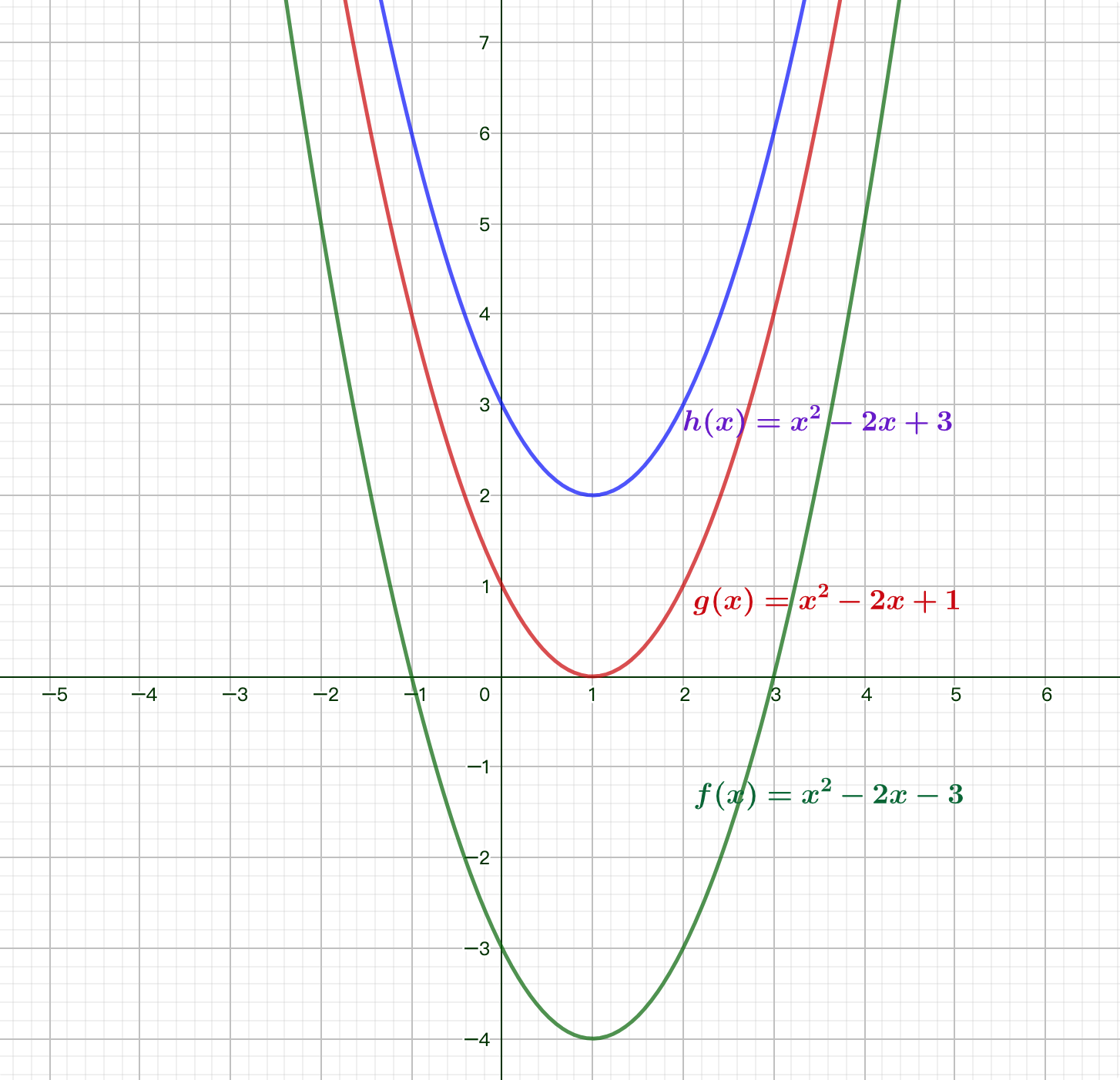
一元二次方程 —— 判别式: 讲解见上面.

根据判别式我们有:

(1) 当时, 一元二次方程有 2 个不等的实数根相应的二次函数的图像与轴有 2 个交点
(2) 当时......
(3) 当时......

二次函数的图像与轴的焦点和相应的一元二次方程的根的关系，可以推广到一般情形，为此，先给出函数零点的概念:

对于函数 , 我们把使的实数叫做函数的 零点(zero point).
这样, 函数的零点就是方程的实数根, 也就是函数的图像于轴的交点的横坐标, 所以 - 方程有实数根函数的图像与 x 轴有交点函数有零点.

一般地, 我们有: 如果函数在区间 [a, b] 上的图像是连续不断的一条曲线, 并且有 , 那么,函数在区间 (a, b) 内有零点, 即存在 , 使得 , 这个也是方程的根.

# 3.2 函数模型及其应用

# 文献阅读与数学写作: 函数的形成与发展

# 小结

# 复习参考题

# ▲ 第 2 章 —— 基本初等函数 (1)

幂函数和指数函数的区别？	示例
幂函数: 底数为自变量，指数为常数。
指数函数: (a > 0 且 ) () 底数为常数, 指数为自变量。

# 2.1 指数函数 (exponential function)

# 2.1.1 指数与指数幂的运算

# (1) 根式

$次方根$ : 一般地如果那么叫做的次方根 (n th root)，其中 , 且

式子叫做 $根式$ (radical), 这里叫做 $根指数$ , 叫做 $被开方数$

例如:

根据 n 次方根的意义可得: ( = .
= 5, = -3.
sqrt = square root 平方根

# (2) 分数指数幂

Tip: 幂: 指乘方运算的结果。指将自乘次 ( 为正整数)。把次方看作乘方的结果，叫做 " $的次幂$ " 或 " $的次方$ "。

我们规定正数的正分数指数幂的意义是:

= ( 且 )[读作: $的分之次方的次方的次方根$ ]

于是，在条件且下, 根式可以写成分数指数幂的形式.

正数的负分数指数幂的意义与负整数指数幂的意义相仿，我们规定

= ( 且 )

0 的正分数指数幂等于 0，0 的负分数指数幂没有意义。

规定了分数指数幂的意义以后，指数的概念就从正数指数推广到了有理数指数。

重要的运算法则: 来源:https://zh.wikipedia.org/wiki/%E5%86%AA

(1) 同底数相乘，底数不变，指数相加: =

(2) 同底数相除，底数不变，指数相减: =

(3) 同指数幂相除，指数不变，底数相除: =

其他等式

=

=

# 2.1.2 指数函数及其性质

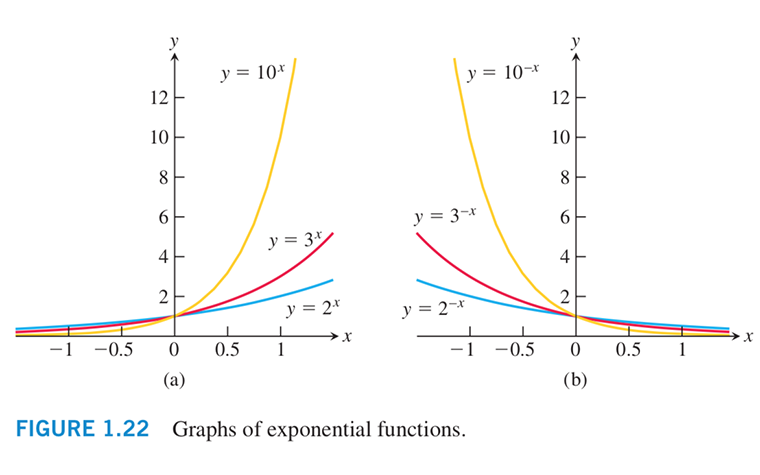
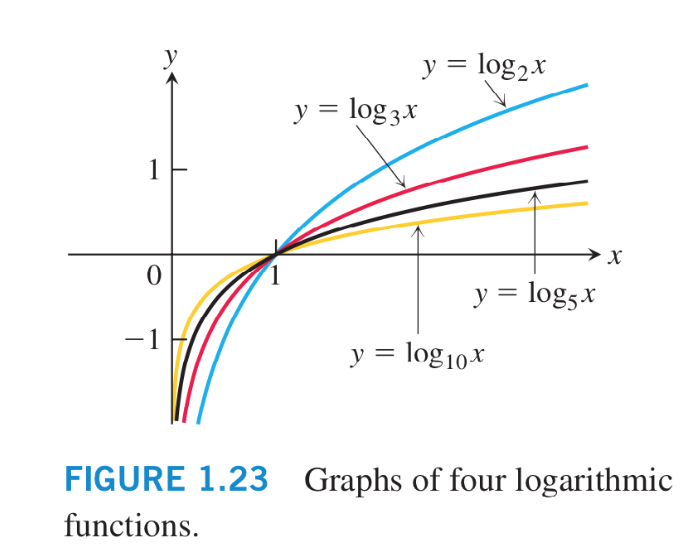
指数函数 (exponential function)}$: 一般地, 函数 $且$ 叫做 "指数函数 (exponential function)"，其中底数为常数, 指数为自变量, 函数的定义域是 .

Add Info: 指数函数 和 对数函数 图形

# 2.2 对数函数 (logarithmic function)

# 2.2.1 对数及其运算

# 对数

$对数$ 一般地，如果 $且$ , 那么数叫做以为底的 "对数(logarithm)", 记作 (读作: 以为底的对数), 其中叫做对数的 "底数"，叫做 "真数"。

$常数对数$ : 通常我们将以 10 为底的对数叫做 "常用对数 (common logarithm)" 并把记作 .

$自然对数$ : 在科学技术中常使用以无理数为底数的对数，以为底的对数称为"自然对数(natural logarithm)",并且把记为。

根据对数的定义，可以得到对数与指数间的关系: 当 $时，$ . 由指数与对数的这个关系，可以得到关于对数的如下结论:

"负数和零都没有对数":
= 0,
= 1.

# 对数的运算

对数的运算性质: 如果 , 且 , , 那么:

(1) = ;
- 读作: 以为底，的对数
(2) = ;
- 同底数幂相减, 底数不变,指数相除
(3) = .

# 对数运算 Wikipedia 公式总结

(1) 和差:

公式: 对数和公式见上面的(1)，对数差公式见上面的 (2)

推导:

对数和公式推导: 设

即:

对数差公式推导:

(2) 基变换 (换底公式)

公式:

推导:

设 两 边 取 对 数 同 底 数 的 对 数 ， 真 数 相 同 ， 对 数 相 等 则 有 即 又 读 作 以 为 底 的 对 数 除 以 以 为 底 的 对 数

(3) 指系 (次方公式)

公式:

推导:

(4) 还原

公式:

推导: 我们由对数的基本定义

把 代 入 右 侧 因 为 ， 所 以 因 此

(5) 互换

公式:

推导:

设 则 有 和 所 以

(6) 倒数:

(7) 链式:

# 2.2.2 对数函数及其性质

$对数函数$ : 我们把函数 y = $且$ 叫做对数函数, 其中是自变量，函数的定义域是。

$反函数$ : 详细见微积分第一章笔记

# 2.3 幂函数 (power function)

★ 必修 4 →

# 数学 (必修) 第一册 A 版 (2021)

# 生词

# ▲ 第 1 章 集合与常用逻辑用语

# 集合[ jí hé ]

# 1.1 集合的概念

# 添加信息 (Add Information)

# 1.2 集合间的基本关系

# 1.3 集合的基本运算

# 1.4 充分条件与必要条件

# (1) 充分条件与必要条件

# (2) 充要条件

# 阅读与思考 几何命题与充分条件、必要条件

# 1.5 全称量词与存在量词

# Add Information:

# 全称量词 / 全称量化

# 基础

# 存在量词 ()

# 1.5.1 全称量词和存在量词

# 1.5.2 全称量词命题和存在量词命题的否定

# 小结

# 复习参考题 1

# ▲ 第 2 章 二次函数 、方程和不等式

# 2.1 等式性质 与 不等式性质

# 2.2 基本不等式

# 2.3 二次函数 与 一元二次方程、不等式

# 小结

# 复习参考题 2

# ▲ 第 3 章 函数的概念与性质

# 3.1 函数的概念及其表示

# 阅读与思考: 函数概念的发展历程

# 3.2 函数的基本性质

# 1.3.1 函数的基本性

# 信息技术应用: 用计算机绘制函数图象

# 3.3 幂函数

# 探究与发现: 探究函数 的图象与性质

# 3.4 函数的应用（一）

# 3.1 函数与方程

# 3.1.1 方程的根与函数的零点

# 3.2 函数模型及其应用

# 文献阅读与数学写作: 函数的形成与发展

# 小结

# 复习参考题

# ▲ 第 2 章 —— 基本初等函数 (1)

# 2.1 指数函数 (exponential function)

# 2.1.1 指数与指数幂的运算

# (1) 根式

# (2) 分数指数幂

# 2.1.2 指数函数及其性质

# 2.2 对数函数 (logarithmic function)

# 2.2.1 对数及其运算

# 对数

# 对数的运算

# 对数运算 Wikipedia 公式总结

# 2.2.2 对数函数及其性质

# 2.3 幂函数 (power function)

# ▲ 第 1 章集合与常用逻辑用语

# 阅读与思考几何命题与充分条件、必要条件

# ▲ 第 2 章二次函数、方程和不等式

# 2.1 等式性质与不等式性质

# 2.3 二次函数与一元二次方程、不等式

# ▲ 第 3 章函数的概念与性质

# 探究与发现: 探究函数的图象与性质